Ground expansion as a numbers game

Pieter Wisse

What follows is inspired by Kent Palmer’s work-in-progress on, as he calls it, General Schemas Theory (GST). Along the way in his (second) dissertation project, Palmer hit upon my model of the semiotic ennead. In draft chapters of dissertation version 0.2 which Palmer kindly shared with me, he has subsequently applied, with comments, the ennead for his own development.
In Notes on metapattern and enneadic semiosis, part 2 I’ve collected some contributions to our correspondence explaining my enneadic design.

Even when I would feel qualified to do full justice to Palmer’s far-reaching effort — which I don’t, not at this moment, anyway; for continued study, I am eagerly awaiting a consolidated version of his theory — a summary of GST lies way beyond the scope of this short paper. Here, I only present the result of my attempt to establish some modifications for ‘steps to an ecology of mind’ on the basis of numerical regularities. As I simply lack Palmer’s impressive command of all that he brings to bear, perhaps I may be excused for doggedly starting from my own original perspective. When somehow relevant, I am sure that Palmer once again can accommodate such a contribution in his metaspeculative project.

Revisiting Schopenhauer’s work in the course of developing the semiotic ennead, I did notice his classification of cause types. I also found it immediately relevant. Over the years, though, my appreciation has deepened (as expressed, for example, in Multiple axiomatization in information management). I fact, their full significance will most probably never become fully clear. Anyway, it is to those cause types that I return here to provide a conceptual ‘zero ground.’ The three cause types are regularly labeled:

1. force
2. impulse
3. sign.

Actually, scientific disciplines may be productively classified accordingly: physics, cybernetics, and significs/semiotics. For each cause type, a particular scientist annex philosopher may be chosen to symbolize it. It could help popular reference. Then, I would argue for Newton to be associated with ‘force,’ Wiener with ‘impulse,’ and Peirce with ‘sign.’
It is a step ‘from nowhere’ to assume cause types. I therefore rank it as zero. Figure 1 sketches the zero-level assumptions as a vector. I refer to the names of Newton, Wiener, and Pierce for arriving at the vector’s analytical representation: {n, w, p}.
Please note, that at zero-level the cause types are considered unitary. It means that the assumption includes the belief that each cause type is totally disjunct from the other cause types.

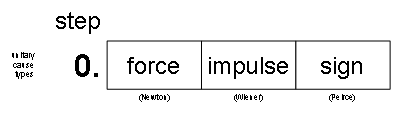
Figure 1: Starting from three unitary cause types.

The first step is to recognize how unitary cause types are actually less unitary than they might appear. In other words, there is already order involved. When force, impulse, and sign are numbered 1, 2, and 3, respectively, as a structural assumption it should be added that a ‘higher’ cause type implies ‘lower’ cause type(s).

A force works directly on an object; effect equals cause.

An impulse is always a force, too. Where an impulse, or Wienerian force, departs from a strictly Newtonian force, however, is how it triggers a disproportionate reaction. The object’s performance relies on some internal structure, necessarily including an energy store. When receptive to impulse, an object is a machine.

A sign is always an impulse, too. Again, the reaction is disproportionate. What makes a sign, or Peircean force, differ from a strictly Wienerian force (impulse) is that it can even shift, say, angle(s). The machine’s performance not only resorts to its energy store. In addition, and characteristically, a store of purposes comes into play. It all turns the machine into an actor.

Figure 2 shows what results from stepping to the first level of ground expansion. Along the horizontal axis, from the first level onwards — with such levels as the vertical orientation for ground expansion, here — the order between the cause types establishes irreducibility. It specifically just means that a Peircean force (sign) may not be reduced to a Wienerian force (impulse), as such an impulse may not be reduced to a Newtonian force. What I have added is — what I hold as — the typical configurations at the first level of ground expansion.

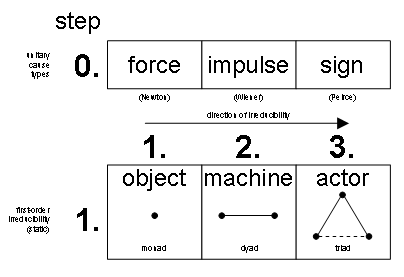
Figure 2: Order of irreducibility between cause types.

At this point, I take my cue from Palmer. At least how I now understand him, in his expansion he limits himself to what I have turned to as cause types #2 and #3. Then, crossing levels, a tetrad and an ennead appear next; see figure 3. Please note that figure 3 is my rendering of an undoubtedly false interpretation of only a small part of a work-in-progress. I would like to emphasize that correctness is not the issue. Often, inspiration comes from insufficient understanding.

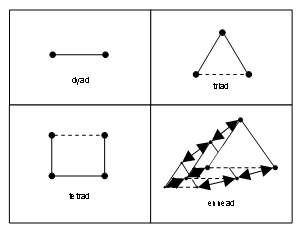
Figure 3: Two adjacent levels in Palmer’s two-dimensional number scheme.

With the number 81 supposedly looming as the result of expansion along the right-hand expansion at the fourth level, Palmer is drawn to establish numerical regularity on the basis of powers. Figure 4 presents an abstraction (with v as the variable for level).

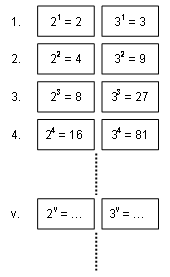
Figure 4: Power levels according to — please note, my interpretation of part of his work-in-progress — Palmer.

So far, there is nothing to suggest why the scheme for ground expansion wouldn’t just comply with Palmer’s. Indeed, what I favor is adding another column to correspond with cause type #1, as shown in figure 5. Actually, in figure 5 I have also included the level of zero-ground which can only add to making our numerical schemes converge.

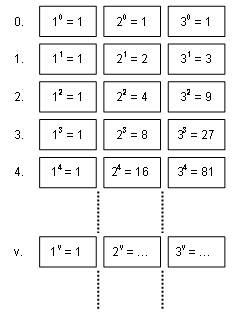
Figure 5: Extending the application of Palmer’s pattern of numerical regularity.

Does this mean that I have done nothing more than rephrasing and slightly extending the reach of Palmer’s numerical rules? I would have been perfectly satisfied with that, except for Palmer’s own reservations about the matrix element figuring the number 27. Let me right away state, as I have already done before, that I lack the knowledge to fathom why Palmer expressed some worry. What’s more, I didn’t see it within my reach to even try to match his incredible learning. But, still, I could sympathize with finding 27 an odd number. Meeting his challenge, though, would mean I had to (re)turn to familiar ground.
It then occurred to me that an alternative regularity could be designed, circumventing what Palmer himself had declared a problematic value. Soon I realized that adding the extra column of singularity at the left-hand side had been important for seizing upon the alternative numerical scheme. Therefore, displaying typical configurations first of all figure 6 recapitulates how I recognize order in ground expansion from zero-ground to the second level of expansion.

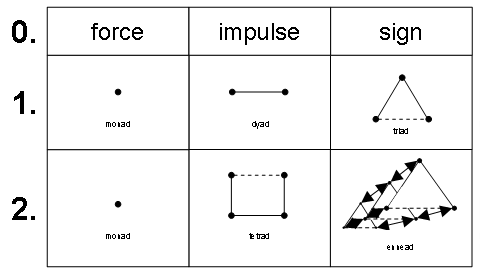
Figure 6: Typical configurations for ground expansion, from zero-ground to second level.

The ‘new’ regularity can only be spotted from the very beginning of ground expansion, which is why figure 6 deserves close scrutiny. At least, what I now find highlighted is that all shown configurations are actually monadic, i.e. their elements are unmistakably derived from monads. This provides the key to what the numbers express. For example, a tetrad is constituted by drawing four elements from the set of monads and subsequently embedding those in an irreducible structure, as a result of which the tetrad ‘emerges’ as a higher-order unit.
The first level is actually unproblematic. An impulse exists in the realm associated with the work of Wiener, so therefore I choose w as the variable. A superscript can indicate the expansion level. The dyad, as the impulse’s typical configuration of the first order, would then be the variable w¹. It is allocated 2 as its monadic expansion number, because its equivalent in monadic terms is: w¹ = {n₁, n₂}. That is, with n₁ and n₂, two elements from the set of monads appear (with n for Newton): monads as nomads. And with p for Peirce, p¹ = {n₁, n_2,n₃}.
Already at this first level, moving in the direction of reduction rather than emergence, a fundamental inquiry of the structure of p¹ suggests itself. Is {n₁, n_2,n₃} reducible to {w¹_,n₃}? It is not. Otherwise there would be no requirement for an additional cause type in the first place.
It is by moving to the second level of ground expansion where the outline of an alternative numerical scheme manifests itself. Concentrating first on the tetrad, how did it occur? Is it a completely novel configuration, as it were delivered straight away as a second-order insight? Thus, w² = {n₁, n_2,n₃, n₄}?
Or is the dyad the necessary intermediate stage toward the tetrad? Is the first step always that w² = { w¹₁, w¹₂}?
I prefer to avoid this question of sequence at this stage. What I emphasize here is how w² actually has two expansion numbers. It has both a dyadic expansion number and a monadic expansion number, 2 and 4, respectively. Please note that the dyadic expansion number for the dyad itself, that is for w¹, is of course 1.
I conclude from the order of irreducibility (see above, figure 2) that the elements of w¹ can only be expanded through substituting dyads for monads. This precisely confirms with Palmer’s numerical prediction, where a power of two is added for each level.
It is for the third cause type, i.e. sign, that I suggest some departure from regularity based on the power of three. It hinges on what qualifies as a substitute. I already proposed, just now, that any monad appearing in a typical configuration for impulse, may be substituted by a dyad. Whether or not there is a practical limit to such expansion, I don’t know.
Anyway, moving to a typical configuration for sign, I argue that the order of irreducibility entails that any monad appearing there may be substituted either by a dyad, or a triad. As I’ll demonstrate shortly, Palmer’s extension by the power of three is thereby modified. And expansion may also result from substituting dyads, of course yielding valid expansion numbers that are not members of the set of powers of three.
The principle of differentiated substitution for sign expansion can immediately applied to the triad. Substituting a dyad for every one of the triad’s monadic elements yields a hexad, that is, the monadic expansion number increases from three to six. And as a result of its expansion history, the hexad also has a dyadic expansion number which is of course three. The original triad has a triadic expansion number of one.
It undoubtedly is an important issue whether or not dyadic and triadic expansion numbers go together. So, does the hexad still have a triadic expansion number? If so, it would be two. But wouldn’t that be mixing categories too much? I am happy to leave — any further — discussion outside the scope of this paper.
Returning to the triad, it can also be expanded by substituting triads for its monadic elements. The resulting ennead’s monadic expansion number is nine — as of course implied by its label, i.e. ennead — and its triadic expansion number is three. (I feel inclined to argue against the ennead having a dyadic expansion number.)
From the two different expansions possible from the triad, a question should be raised pertaining to distinct levels. In Palmer’s scheme no ambiguity occurs as the level is simply determined by the power of both two and three, vice versa. But deserve both the hexad and the ennead being placed at the same ‘level’?
Or should the concept of level be maintained, but the rules for substitution made more precise? I favor this alternative, because I still need to make sure that 27 does not hold as a expansion number. Please note that it is now more accurate to call it a monadic expansion number.
For developing a further alternative, figure 7 shows derivations at the first and second level (which is to say that, at least for the moment, I stick to levels of ground expansion).

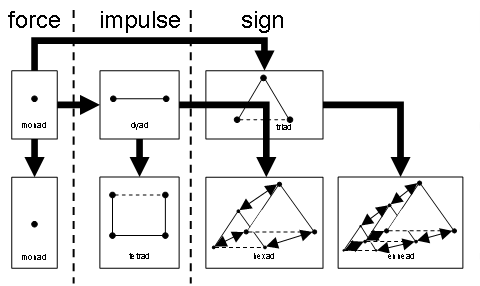
Figure 7: Actual derivations from monad to ennead.

What this suggests to me — I admit, set against the requirement of avoiding the number 27 — is declaration of progression in substitution. Let me start to explain it for impulse expansion, as it still proceeds along a single path. There, the rule could be that any typical configuration could only ‘feed’ itself. So, specifically for the tetrad, in order to expand to the next level a tetrad must be substituted for all of its elements. This way, expansion skips the third power of two and ‘jumps’ to four times four make sixteen for its monadic expansion number.
Does this make sense? Frankly, I myself honestly couldn’t answer right now either way. Would it still facilitate inquiry when the tetrad’s elements are replaced by dyads? Or is the dyad’s productivity already exhausted by lifting itself up, i.e. emerging as tetrad through, indeed, self-expansion? I’m out of my depth because I find practical illustrations wanting which I sorely need to at least convince myself. Then again, it always is a theory that offers a particular perspective. Most likely, we again need time to learn to ‘see’ differently.
Turning to sign expansion, as the dyad could be applied to the triad, it seems reasonable to assume that the tetrad can be used for substituting all of the hexad’s elements. Monadically, four times six make twenty-four.
Also, the hexad could be self-expanding: thirty-six. Or the hexad applied to the ennead for expansion: fifty-four. The final possibility arriving at the third level is the ennead’s self-expansion: eighty-one.
In terms of avoiding twenty-seven, the new rules really work.
It now remains to formalize the rules, where I limit myself here to the monadic expansion numbers. What such actual numbers have actually been inferred, so far? Figure 8 shows the results.

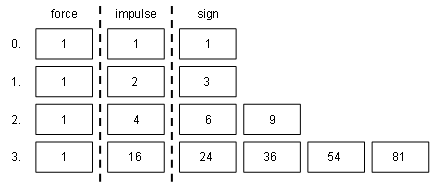
Figure 8: Monadic expansion numbers for the levels zero to three.

Well, I don’t have the stomach right now to develop the generalized formula(s). For the moment, I am content with the formula for self-expansion. See figure 9.

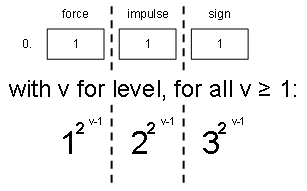
Figure 9: The formula for self-expansion with variable level, yielding the relevant monadic expansion number.

Given the numbers for the cause types, it’s straightforward to even enhance generalization for self-expansion, as given in figure 10.

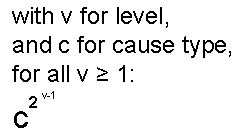
Figure 10: Self-expansion formula with both level and cause type as variables.

All the other expansions probably are unstable, anyway, as I myself experienced with the hexad which I continued to develop into the semiotic ennead. I also believe that the constraint of self-expansion keeps my numerical scheme optimally aligned with Palmer’s.
Please note that my concept of self-expansion limits substitutes for monads to the next-lower level typical configuration for the same cause type; see figure 11.

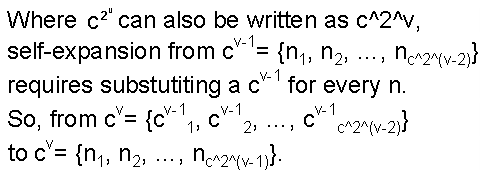
Figure 11: Self-expansion defined.

What I have tried to demonstrate in this paper is how the numbers game of ground expansion can be productively structured with just three unitary cause types as the basic ingredients at zero level. Is has been an exercise in ontology, a word which I wanted to save for this last sentence (and succeeded).